Linux-Magazin-Logo Die Zeitschrift für Linux-Professionals
  Home
   Artikel > August > Algebra für Rechenmuffel

Zwei Perl-Module helfen mathematische Funktionen zu lösen und darzustellen

Algebra für Rechenmuffel

Michael Schilli
Millionen Schülern graust es vor dem Algebra-Unterricht. Gewiefte Eleven zücken nicht bei jeder mehr oder weniger komplexen Rechenaufgabe ihr Formelbüchlein - sondern Perl. Zwei Module sorgen dafür, Gleichungen aufzustellen und zu lösen sowie ansprechende Formelgraphen zu zeichnen.

Das Rechnen mit der Variablen x zieht sich durch alle Lebenslagen: ob Benzinverbrauch oder eine Fuchs-und-Hase-Jagd, überall kommen die Grundsätze der Algebra zur Geltung. Wie gut, dass es Perl gibt, denn dank eines entsprechenden Moduls übernimmt ein Skript das Lösen und Umformen von Gleichungen. Beispiele zeigen im Folgenden, was dies Modul alles kann.

Benzinschleudern auf Amerikanisch

Als erste Aufgabe dient eine einfache Formel: In den USA geben Autohersteller nicht an, wie viele Liter Benzin ihre Vehikel auf 100 Kilometer verbrauchen, sondern wie viele Meilen diese mit einer Gallone Benzin fahren. Ein hoher Wert indiziert also niedrigen Benzinverbrauch. Die Aufgabe besteht nun darin, einen Meilen-pro-Gallone-Wert in Liter pro 100 Kilometer umzurechnen. Das Skript Mpgal in Listing 1 nutzt das Perl-Modul »Math::Algebra::Symbols« und definiert die zwei Symbole »$gallons« und »$miles«. Ab Zeile 14 baut es die Formel Schritt für Schritt auf.

Listing 1: »mpgal« 

01 #!/usr/bin/perl
02 ###########################################
03 # mpgal - miles/gallon => liters/100km
04 # Mike Schilli, 2004 (m@perlmeister.com)
05 ###########################################
06 use warnings;
07 use strict;
08 
09 use Math::Algebra::Symbols;
10 
11 my ($gallons, $miles) =
12    symbols(qw(gallons miles));
13 
14 my $liters = $gallons * 37854118/10000000;
15 my $kilometers = $miles * 1609344/1000000;
16 my $usage = $liters / $kilometers * 100;
17 
18 print "Formula: $usage\n";
19 
20 for $miles (qw(20 30 40)) {
21 
22     $gallons = 1;
23 
24     printf "$miles m/gal: " .
25            "%4.1f l/100km\n", eval $usage;
26 }

Der Ausdruck in Zeile 14 gibt an, dass eine Gallone 3,7854118 Litern entspricht. Zwei Dinge sind zu beachten: Erstens mag Math::Algebra::Symbols in der aktuellen Version 1.16 keine langen Fließkommawerte, weshalb Programmierer sie als Bruch angeben müssen. Zweitens gibt »$liters« die Anzahl der Liter im Beispiel an. Daher ist es nötig, die Anzahl der Gallonen mit 3,7854118 zu multiplizieren: 2 Gallonen (eine 2 für »$gallons«) entsprechen also 7,5708236 Litern (in »$liters«). Ähnliches gilt für Kilometer und Meilen, eine Meile entspricht 1,609344 Kilometern.

Den Benzinverbrauch pro 100 Kilometer berechnet die Formel in Zeile 16. Da für »$liters« und »$kilometers« im Skript bereits Formeln definiert sind, ersetzt Math::Algebra::Symbols die Symbole und generiert eine Gleichung, die nur noch von »$gallons« und »$miles« abhängt. Zeile 18 gibt sie aus: 

Formula: 94635295/402336*$gallons/$miles

Math::Algebra::Symbols hat dazu mit ein wenig Bruchrechnung die vorher definierten Konstanten gekürzt. Um konkrete Werte in die Formel einzusetzen, weist Mpgal den Variablen »$gallons« und »$miles« Werte zu (in diesem Beispiel 20, 30 und 40) und ruft in Zeile 25 jeweils »eval $usage« auf, um die Formel anzuwenden: 

20 m/gal: 11.8 l/100km
30 m/gal:  7.8 l/100km
40 m/gal:  5.9 l/100km

Dieses Beispiel ist allerdings nur der Anfang, eine einfache Funktion direkt in Perl hätte es hier ebenfalls getan. Das Modul Math::Algebra::Symbols kann aber auch Gleichungen höheren Grades nach Variablen auflösen, wie das nächste Beispiel zeigt.

Der Fuchs jagt den Hasen

Die zweite Aufgabe, die das Perl-Modul lösen soll, ist eine klassische Textaufgabe: Ein Fuchs sieht einen in 10 Metern Entfernung und mit einer Geschwindigkeit von konstanten 5 Metern pro Sekunde flüchtenden Hasen und beginnt die Hatz. Dabei beschleunigt der Fuchs mit 7 Metern pro Sekundequadrat. Wie lange dauert es, bis er den Hasen schnappt und welche Strecke muss er dabei zurücklegen?

Das Programm Race in Listing 2 definiert hierzu das Symbol »$t« für die verstrichene Zeit in Sekunden und gibt die von Hase und Fuchs jeweils gelaufene Strecke an, abhängig von der Zeit (Zeilen 13 und 14): 

my $rabbit = 10 + 5 * $t;
my $fox    =      7 * $t * $t;

Listing 2: »race« 

01 #!/usr/bin/perl
02 ###########################################
03 # race - Fox chasing a Rabbit
04 # Mike Schilli, 2004 (m@perlmeister.com)
05 ###########################################
06 use warnings;
07 use strict;
08 
09 use Math::Algebra::Symbols;
10 
11 my ($t) = symbols(qw(t));
12 
13 my $rabbit = 10 + 5 * $t;
14 my $fox    =      7 * $t * $t;
15 
16 my $schnapp = ($rabbit - $fox);
17 
18 for my $solution
19     (@{$schnapp->solve("t")}) {
20     print "Solution: $solution\n";
21     my $val = eval $solution;
22     if($val < 0) {
23         print "Discarded\n";
24         next;
25     } else {
26         printf "%.2f seconds\n", $val;
27         $t = $val;
28         printf "%.2f meters\n", eval $fox;
29     }
30 }

Der Hase hat mit seinen 10 Metern Vorsprung und gemäß der Formel für konstante Geschwindigkeit (s=v*t) nach t Sekunden die Strecke 10+5[m/s]*t zurückgelegt, während der Fuchs gemäß der Formel für konstante Beschleunigung (s=a*t2) genau 7[m/s2]*t2 Meter schafft. Er schnappt den Hasen, wenn beide Streckenangaben übereinstimmen, die Gleichung von Zeile 16 also den Wert null liefert.

Von Hand ausgerechnet liefe dies auf eine quadratische Gleichung hinaus - ich jedenfalls müsste wieder mein Formelbuch der siebten Klasse aus dem Keller holen. Aber dank Math::Alge- bra::Symbols lässt sich die Variable »$schnapp« einfach mit der Modul-Methode »$schnapp->solve("t")« nach »$t« auflösen. Diese Methode liefert (wegen der quadratischen Gleichung) eine Liste mit zwei symbolischen Gleichungslösungen zurück (ab Zeile 19): 

Solution: 1/14*sqrt(305)+5/14
Solution: -1/14*sqrt(305)+5/14

Da negative Zeiten für praktische Belange wie das Leben des Hasen irrelevant sind, verwirft Race die zweite Lösung mit dem Code ab Zeile 23. Den Lösungswert in Sekunden erhält der Programmierer dann durch Einsetzen, was wie im vorigen Beispiel das Perl-Konstrukt »eval« erledigt (Zeile 21).

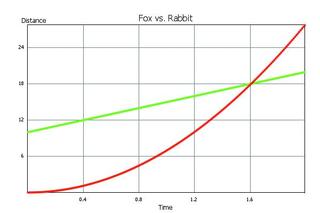
Nach etwa 1,60 Sekunden ist's also aus mit dem Hasen und nachdem Zeile 27 »$t« auf dieses Ergebnis gesetzt hat, steht auch die vom Fuchs zurückgelegte Strecke fest: »eval $fox« gibt sie mit etwa 18,02 Metern an.

Grafisch aufpoliert

Listing 3 illustriert das Ganze schließlich grafisch, wie in Abbildung 1 zu sehen. Mit dem Modul »Imager::Plot« lassen sich mit ein paar Zeilen Perl-Code professionelle Plots in verschiedenen Bildformaten zeichnen. Zeile 12 erzeugt ein neues »Imager::Plot«-Objekt in entsprechender Größe und nutzt für die Beschriftung der Graphen den unter dem angegebenen Pfad stehenden Truetype-Font »tahoma.ttf«.

Abbildung 1: Nach etwa 1,6 Sekunden schnappt der Fuchs den mit 10 Metern Vorsprung und konstanter Geschwindigkeit rennenden Hasen. Zwei Perl-Module ermöglichen die schnelle Funktionserstellung und die grafische Auswertung.

Listing 3: »graph« 

01 #!/usr/bin/perl
02 ###########################################
03 # graph -- Graph of fox/rabbit chase
04 # Mike Schilli, 2004 (m@perlmeister.com)
05 ###########################################
06 use strict;
07 use warnings;
08 
09 use Imager;
10 use Imager::Plot;
11 
12 my $plot = Imager::Plot->new(
13   Width  => 550,
14   Height => 350,
15   GlobalFont =>
16   '/usr/share/fonts/truetype/tahoma.ttf');
17 
18 my (@t, @rabbit, @fox);
19 
20     # Generate function data
21 for(my $i = 0.0; $i < 2.0; $i += 0.01) {
22     push @t, $i;
23     push @rabbit, 10 + 5 * $i;
24     push @fox, 7 * $i * $i;
25 }
26 
27     # Add rabbit plot
28 $plot->AddDataSet(X => \@t, Y => \@rabbit,
29   style => {
30     marker => {
31       size   => 2,
32       symbol => 'circle',
33       color => Imager::Color->new('green')
34 }});
35 
36     # Add fox plot
37 $plot->AddDataSet(X => \@t, Y => \@fox,
38   style => {
39     marker => {
40       size   => 2,
41       symbol => 'circle',
42       color  => Imager::Color->new('red')
43     }});
44 
45 my $img = Imager->new(xsize => 600,
46                       ysize => 400);
47 
48 $img->box(filled => 1, color => 'white');
49 
50     # Add text
51 $plot->{'Ylabel'} = 'Distance';
52 $plot->{'Xlabel'} = 'Time';
53 $plot->{'Title'}  = 'Fox vs. Rabbit';
54 
55 $plot->Render(Image => $img,
56     Xoff => 40, Yoff => 370);
57 
58 $img->write(file => "graph.png");

Die »for«-Schleife ab Zeile 21 iteriert in Hundertstel-Schritten über x-Werte von 0,0 bis 2,0 und legt drei Arrays an: »@t« für die x-Achsenwerte und »@rabbit« beziehungsweise »@fox« für die Ortswerte von Hase und Fuchs. Diese Ortsangaben sind den jeweiligen Zeitwerten gemäß den Bewegungsformeln von Fuchs und Hase zugeordnet.

Zeile 28 fügt den grünen Hasen-Plot in das Koordinatensystem ein, Zeile 37 und folgende fügen den Graphen des Fuchses in Rot hinzu. Die »Render()«-Funktion in Zeile 55 übernimmt das Zeichnen und »write()« in Zeile 58 schreibt das Ganze in eine PNG-Datei.

Kurvendiskussion

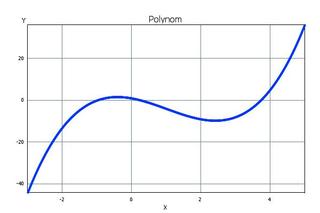
Auch mit dieser Aufgabe ist der Funktionsumfang von Math::Algebra::Symbols noch nicht ausgeschöpft, denn das Modul beherrscht auch Kurvendiskussionen. Abbildung 2 zeigt den Kurvenverlauf des Polynoms y=x3-3x2-3x+1, dessen zwei Ausschläge jeweils ein lokales Maximum und Minimum bilden. In der Schule habe ich gelernt, dass die Steigung der Kurve an diesen Stellen gleich null ist. Um sie zu bestimmen, differenziert man die Funktion, setzt das Ergebnis gleich null und bestimmt die Lösungen der entstehenden Gleichung. Glücklicherweise beherrscht Math::Algebra::Symbols die Differenzierung von einfachen Funktionen: 

my ($x) = symbols('x');

my $y = $x**3 - 3*$x**2 - 3*$x + 1;
my $diff = $y->d('x');

my $extrema = $diff->solve('x');
print eval($_), "\n" for @$extrema;

Abbildung 2: Der Funktionsverlauf des Polynoms y = x3-3x2-3x+1. Das Perl-Modul »Math::Algebra::Symbols« hilft rechenfaulen Programmierern, bei derartigen Funktionsgraphen Kurvendiskussionen durchzuführen.

Die Methode »$y->d('x')« differenziert die in »$y« definierte Funktion nach »$x«, was das angegebene Polynom dritten Grades in eines zweiten Grades überführt. Die nachfolgend aufgerufene »solve()«-Methode löst Letzteres und gibt wie vorher eine Referenz auf ein Array mit zwei Elementen zurück. Diese rationalen Zahlen konvertiert die »eval«-Funktion in die Fließkommawerte: 

-0.414213562373095
2.41421356237309

Das sind die x-Werte der Extrema. Um die y-Werte zu erhalten, setzt man die Variable »$x« gleich dem evaluierten Wert für das jeweilige Extremum und wertet anschließend »$y« aus: 

for(@$extrema) {
  $x = eval $_;
  print eval($y), "\n";
}

Auch der Wendepunkt eines Graphen zwischen zwei Extrema lässt sich sehr einfach bestimmen. Er ist die Grenze zwischen abnehmender und zunehmender Steigung. Die zweite Ableitung ist dort gleich null. Der Ausdruck »$y->d('x')->d('x')->solve('x')« gibt für das oben angegebene Polynom exakt den x-Wert 1 zurück. Math::Algebra::Symbols beherrscht auch trigonometrische Funktionen, kommt bei komplizierteren Strukturen aber noch ins Schleudern.

Vorsicht, Baustelle!

Math::Algebra::Symbols und Imager::Plot sind vom CPAN erhältlich und eignen sich hervorragend zum Herumspielen mit allerlei mathematischen Rätseln. Math::Algebra::Symbols ist noch Alpha-Qualität, wird aber von seinem Autor Philip Brenan stetig weiterentwickelt und könnte im Laufe der Zeit immer mehr Funktionen anbieten, ähnlich wie Mathematica. Das Fazit dieser kleinen Mathestunde steht schon jetzt fest: Wer fleißig Mathe paukt, der lernt was fürs Leben! (mwe)

Infos

[1] Listings zu diesem Artikel: [ftp://ftp.linux-magazin.de/pub/listings/magazin/2004/08/Perl]

Der Autor

Michael Schilli arbeitet als Software-Engineer für AOL/Netscape in Mountain View, Kalifornien. Er hat "Goto Perl 5" (deutsch) und "Perl Power" (englisch) für Addison-Wesley geschrieben, er ist unter [mschilli@perlmeister.com] zu erreichen und seine Homepage heißt [http://perlmeister.com].