


|

|
|
|
Autonome Entscheidungsfindung bei RoboternPlanwirtschaftAlexander Ferrein |

|
Ein Roboter steht allein vor dem gegnerischen Tor, kein Gegner in Reichweite, er müsste einfach nur schießen - doch er tut es nicht. Seine Programmierer raufen sich die Haare und verstehen selbst nicht, warum die verflixte Maschine nicht schießt. Für uns Menschen ist die Sache klar, wir erkennen das leere Tor und halten drauf.
Einem Roboter fällt die Entscheidung deutlich schwerer. Zunächst muss er seine Umgebung wahrnehmen, er nutzt dazu verschieden Sensoren wie Kamera, Laser-Scanner, Sonar oder Gyroskop. Die Spielbedingungen sind bekannt: Das Feld, Tore mit gelbem und blauem Hintergrund sowie weißen Eckpfosten, es gibt weiße Linien auf grünem Teppich und der Fußball ist orange. Aus den Sensorwerten muss der Roboter seine Welt erkennen, modellieren und auf dieser Basis Entscheidungen fällen.
Das Weltmodell beinhaltet Daten wie die Positionen des Roboters, der Mitspieler, der Gegner und des Balls. Diese Objekte zu erkennen ist schwierig, da die Sensordaten immer Fehler enthalten, etwa weil die Kamera nicht richtig kalibriert ist und falsche Farben zeigt. Dies führt zu falschen oder ungenauen Schätzungen der Informationen im Weltmodell. Im schlimmsten Fall glaubt der Roboter, an einer anderen Position zu stehen. Ausgereifte Techniken wie die Monte-Carlo-Methode oder Kalman-Filter minimieren solche Unsicherheiten; Grundprobleme der Robotik wie Lokalisierung sind dennoch nicht abschließend gelöst.
Aus den Sensorendaten leitet der Roboter weitere wichtige Informationen ab. Beispiele hierfür sind die Distanz zum gegnerischen Tor oder der Öffnungswinkel zum freien Torbereich. Damit entscheidet der Roboter, wie er sich verhält. Das folgende C-Listing implementiert einen Entscheidungsbaum für die in Abbildung 1 gezeigte Situation:
if (DistanceToGoal > 1.5)
dribbleToGoal();
else {
if (AngleBetween(goalKeeper, goalPost) > 0.35)
shootAtGoal();
else
turnLeft();
}
Ist die Distanz zum Tor größer als 1,5 Meter, dribbelt der Roboter näher zum Tor. Ansonsten prüft er, ob der Winkel zwischen Torwart und Torpfosten größer als 20 Grad ist, und schießt. Das scheint für die abgebildete Situation zu funktionieren. Steht hingegen der blaue Spieler Nummer 2 aus Abbildung 1 zwischen Angreifer und Tor, wäre ein Schuss vergeblich - die Position des gegnerischen Roboters ist in diesem Entscheidungsbaum aber nicht berücksichtigt, der Angreifer schießt trotzdem.
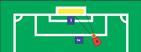
Diese unnötigen Torschussversuche lassen sich vermeiden, wenn die Winkelberechnung mögliche Gegner mit einbezieht - falls die Sensoren überhaupt Gegner erkennen. Ein weiteres Problem ist, dass die Torfarbe unberücksichtigt bleibt, der Roboter könnte also, ohne es zu merken, ein Eigentor fabrizieren. Auch diesen Umstand berücksichtigen erfordert weiteren Code.
Das Beispiel zeigt, wie wichtig der Aufbau des Weltmodells ist. Die Entwickler dürfen keine relevanten Informationen übersehen, das Modell aber auch nicht überfrachten. Das Beispiel setzt voraus, dass ein Weltmodell mit Daten wie »DistanceToGoal« oder Aktionen wie »dribbleToGoal()« existiert. Das beschreibt jedoch nur einen möglichen Lösungsansatz, der eine bestimmte Systemarchitektur erfordert.
Die Roboter-Forscher teilen ihre Ansätze in drei grundlegende Architektur-Paradigmen ein: das reaktive Paradigma, das hierarchische Paradigma und das hybride Paradigma. Beim reaktiven Paradima sind die Sensoren direkt mit den Aktuatoren gekoppelt. Der Roboter aktiviert seinen Motor immer für eine bestimmte Zeit, wenn der Sensor einen bestimmten Wert misst. Hier braucht die Entscheidungsfindung kein Weltmodell, alle Aktuatoren reagieren direkt auf Sensor-Stimuli.
Reaktive Steuerungen arbeiten sehr schnell, mehr als ein Table-Lookup oder ein kurzer Entscheidungsbaum sind nicht nötig. Allerdings können Roboter nach reaktivem Paradigma auf unbekannte Situationen oder Ereignisse nicht angemessen reagieren. Zudem verhalten sie sich bei gleichen Stimuli stets identisch, sind also sehr berechenbar.
Im Gegensatz dazu steht das hierarchische Paradigma. Hier bildet der Roboter ein Modell seiner Umgebung und führt abstrakte Aktionen im Weltmodell aus. Das zentrale Element ist eine Planungskomponente. Ausgehend vom Weltmodell plant sie eine Aktionsfolge, um ein bestimmtes Ziel zu erreichen. Als Ziel könnte ihr "Schieße ein Tor" vorgeben sein. Die Entscheidungsfindung läuft bei diesem Paradigma in drei Schritten ab: Erkennen, Planen, Ausführen.
Das hybride Paradigma vereint beide Ansätze, indem es die Planungskomponente von der Ausführung abkoppelt und den starren Ausführungszyklus Erkennen, Planen und Ausführen aufbricht. Dadurch kann der Roboter auf wichtige Ereignisse direkt reagiert, andererseits aber auch längerfristige Pläne verfolgen.
Die Wissenschaft kennt viele Ansätze, um intelligente Entscheidungen zu treffen. Sie unterscheidet zwischen reaktiven und deliberativen (Plan-basierten) Ansätzen. Deliberativ bedeutet, dass der Roboter ausgehend von der aktuellen Situation eine Sequenz von Aktionen berechnet, die ihn ein irgendwie formuliertes Ziel erreichen lässt. Dabei muss er die nächsten sinnvollen Aktionen vorausberechnen.
Dieser Vorgang ist wesentlich aufwändiger und dauert länger als bei der reaktiven Methode. Plan-basiert lassen sich dafür Strategien formulieren, die Ziele erreichen, die rein reaktiv unerreichbar wären. Das Problem: In einer Echtzeit-Umgebung wie einem Robocup-Turnier bleibt nur wenig Zeit zum Grübeln.
Der Grundgedanke beim Lernen eines Entscheidungsbaums ist einfach: In jeder Situation gibt es eine beste Aktion, die der Roboter ausführen sollte. Diese lernt er, indem der Entwickler für eine Vielzahl von Beispielsituationen die aus menschlicher Sicht jeweils optimale Entscheidung vorgibt. Später ruft das Gerät in gleichen Situationen nur die gelernte Aktion ab und führt sie aus.
Leider gibt es beim Robocup zu viele verschiedene Situationen, um alle zu modellieren - meist sogar unendlich viele. Die Merkmale der Welt, mit denen Roboter ihre Situation beschreiben, sind in der Regel kontinuierlich. Zum Beispiel die Position, für sie sind zwei Fließkommawerte nötig. Auch eine einfache Diskretisierung, etwa in 10-Zentimeter-Schritten für die eigene Position, genügt meist nicht, um den Zustandsraum auf eine handhabbare Größe zu reduzieren.
Hier greift das Entscheidungsbaum-Lernen. Der Entwickler trainiert den Roboter nur an einer begrenzten Menge von Beispielen, die möglichst viele, subjektiv verschiedene Zustände abdecken. Davon abstrahiert der Roboter, um auch solche Zustände abzudecken, die er im Training nicht erlebt hat.
Der Entwickler arrangiert zum Beispiel im Training mehrere Situationen, in denen der Roboter schießen soll. Diese Situationen haben alle gemeinsam, dass wie in Abbildung 1 der Weg zum Tor frei und der Roboter in Ballbesitz ist - dafür steht er aber immer an einer anderen Position. Daraus leitet der Lernalgorithmus im Idealfall ab, dass die Position des Roboters und möglicherweise andere Merkmale der Welt in diesem Fall nicht relevant sind. Die Maschine merkt sich als Regel für später: Wenn der Weg zum Tor frei und der Roboter in Ballbesitz ist, schießt er.
Mit diesem Verfahren kann der Entwickler sehr effektiv seine Vorstellung vom gewünschten Verhalten seines Roboters umsetzten. Jedoch ist der Aufwand recht groß, da der Trainer viele Beispiele durchgehen muss, in der Middle Size League bis zu mehreren hundert. Außerdem wird es mit wachsender Komplexität des Spiels immer schwerer, die tatsächliche Bandbreite der möglichen Zustände abzudecken, genau wie beim reaktiven Paradigma. Weitere Informationen zum Entscheidungsbaum-Lernen gibt es unter[1].
Beim Reinforcement Learning gibt es keinen Lehrer, der dem Roboter vorgibt, welche Aktion in welcher Situation gut oder schlecht ist, sondern ein Bewertungssystem, das den Ausgang einer Aktion bewertet (Reward-Funktion). Während der Lernphase probiert der Roboter allerlei Aktionen durch und merkt sich, welche zu einer gut bewerteten Situation geführt haben. So lernt er das gewünschte Verhalten und entwickelt eine eigene Policy, die Situationen auf Aktionen abbildet. Mit ihr ist er in der Lage, zu einer gegebenen Situation eine geeignete Aktion auszuwählen.
Mit Hilfe der Reward-Funktion kann der Roboter in jeder Situation feststellen, ob der aktuelle Zustand wünschenswert ist oder nicht. Je höher die Bewertung des Zustands ausfällt, desto wünschenswerter ist er. Allerdings kommt es durchaus vor, dass die Maschine zunächst einen schlechten Zustand in Kauf nehmen muss, um danach einen guten zu erreichen. Mit der Bewertungsfunktion allein bliebe der Roboter möglicherweise in einem lokalen Bewertungsminimum stecken. Daher gibt es die Value-Funktion, sie liefert die erwartete Bewertung am Ende einer komplexen Aktion.
Formal ausgedrückt maximiert das System den Erwartungswert des kumulierten Rewards. Erwartungswert deshalb, weil die zugrunde liegende MDP-Theorie (Markov Decision Process,[2]) wahrscheinlichkeitsbehaftete Zustandsübergänge erlaubt. Das bedeutet, dass man durch eine Aktion (Zustandsübergang) mit einer gewissen Wahrscheinlichkeit p1 in einen Zustand z1 gelangt und mit einer Wahrscheinlichkeit p2 im Zustand z2 landet. Mit Hilfe der MDP-Theorie kann der Roboter die Unsicherheiten beim Ausführen einer Aktionen einkalkulieren.
| Listing 1: Auszug aus dem Angreifer-Programm |
|
01 solve(nondet( 02 [kick(ownNumber, 40), 03 dribble_or_move_kick(ownNumber), 04 dribble_to_points(ownNumber), 05 if(isKickable(ownNumber), 06 pickBest(var_turnAngle, [-3.1, -2.3, 2.3, 3.1], 07 [turn_relative(ownNumber, var_turnAngle, 2), 08 nondet([[intercept_ball(ownNumber, 1), 09 dribble_or_move_kick(ownNumber)], 10 [intercept_ball(no_ByRole(supporter), 1), 11 dribble_or_move_kick(no_ByRole(supp.))]]) ]), 12 nondet([[intercept_ball(ownNumber, 1), 13 dribble_or_move_kick(ownNumber)], 14 intercept_ball(ownNumber, 0.0, 1)]) 15 ) ]), 4) 16 17 proc(dribble_or_move_kick(Own), 18 nondet([[dribble_to(Own, oppGoalBestCorner, 1)], 19 [move_kick(Own, oppGoalBestCorner, 1)]])). 20 21 proc(dribble_to_points(Own), 22 pickBest( var_pos, 23 [[2.5, -2.5], [2.5, 0.0], [2.5, 2.5]], 24 dribble_to(Own, var_pos, 1))). |
Beim Reinforcement Learning kennt der Roboter eine Beschreibung seiner Umgebung und kann zwischen verschiedenen Aktionen wählen. Die Bewertungsfunktion liefert ihm eine Einschätzung seines gegenwärtigen Zustands. Der Roboter probiert mehrere Aktionen durch und versucht dann, eine möglichst gute Bewertung zu erreichen.
Eine gute Einführung in diesen Lernalgorithmus gibt das Buch von Sutton und Barto[3]. Das Aachener Robocup-Team Allemaniacs verfolgt den deliberativen und den reaktiven Ansatz[9]. Die Kombination verspricht, dass die Roboter langfristige, strategische Ziele verfolgen, ohne auf schnelle Reaktionen verzichten zu müssen.
In der Planungsphase legt der Roboter eine Reihenfolge von Aktionen fest, die zu einem bestimmten Ziel führen soll. Die Grundfunktionen des Roboters haben zum Teil Vorbedingungen, die erfüllt sein müssen, und Auswirkungen auf die Umwelt. Beides muss das Planungssystem berücksichtigen.
Das Hauptziel im Fußball sollte immer "Gewinne das Spiel" lauten, allerdings ist das für jedes Planungssystem zu allgemein gehalten. Die Entwickler müssen erfüllbare Teilziele vorgegeben, zum Beispiel "Bringe den Ball in das gegnerische Tor". Das Planungsmodul berechnet mit Hilfe dieser Zielvorgabe und den jeweils möglichen Aktionen einen Ablauf, der zum Ziel führt.
Die Roboter der Allemaniacs Aachen benutzen eine Form des entscheidungstheoretischen Planens. Statt einer expliziten Zielvorgabe greifen sie auf die Optimierungstheorie zurück, um ihre Aktionssequenz zu planen. Sie bewerten ihre aktuelle Situation mit einer Reward-Funktion und sagen mit Hilfe einer formalen Beschreibung vorher, welcher Zustand nach dem Ausführen einer Aktion herrschen wird.
Da der Roboter - wie seine menschlichen Kollegen auch - nicht alles berücksichtigen kann, was auf dem Fußballfeld passiert, muss er vereinfachende Annahmen treffen. Das Planungsystem berechnet ausgehend von der aktuellen Sicht der Welt die Aktionsfolge mit dem besten Wert - mit dem Ziel, den Ball ins gegnerische Tor zu schießen.
Die Suche ist schwierig, da ein Roboter nicht immer jede gewünschte Aktion ausführen kann. Wenn in Abbildung 1 ein Gegner zwischen Ball und Tor steht, kann der rote Spieler mit der Nummer 4 kein Tor schießen. Zudem haben die Aktionen, die der Roboter ausführt, keine deterministischen Effekte: Schießt er den Ball in zwei unterschiedlichen Situationen, landet er nicht immer an der gleichen Stelle. Mögliche Ursachen sind, dass der Roboter in einem leicht anderen Winkel zum Ball steht oder dass der Boden eine Welle hat.
Diese Ungenauigkeiten im Weltmodell lassen sich stochastisch beschreiben. Der Ball wird nach einem Schuss mit einer gewissen Wahrscheinlichkeit an dieser und mit einer anderen Wahrscheinlichkeit an jener Stelle landen. Die Stochastik definiert über alle modellierten Effekte einer Aktion eine Wahrscheinlichkeitsverteilung, um der Unsicherheit der Umwelt Rechnung zu tragen. Die formale Theorie dahinter ist wieder der Markov Decision Process. Das Planungssystem muss die Unsicherheiten und alle möglichen Effekte einer Aktion einkalkulieren.
Die Aktionssequenz, die ein gutes Planungssystem vorschlägt, maximiert den Erwartungswert des kumulierten Rewards. Eine solch komplexe Planung ist sehr zeitaufwändig, weshalb man in harten Echtzeit-Umgebungen wie dem Robocup den Suchraum für das Planungssystem einschränkt.
Für die Spezifikation der Robotersteuerung benutzen die Allemaniacs die Sprache Golog[4]. Sie basiert auf dem Situationenkalkül[5], einer Logik zweiter Stufe. In Golog ist es möglich, über Aktionen und deren Effekte logisch nachzudenken. Golog nimmt an, dass Veränderungen der Welt nur durch Aktionen hervorgerufen werden. Durch Ausführen einer Aktion gelangt ein System von einer Anfangssituation S0 in eine andere Situation.
Die Veränderungen der Welt lassen sich somit als eine Aktionssequenz ausgehend von S0 darstellen. Eigenschaften der Welt werden durch so genannte Fluenten beschrieben. Fluenten sind Relationen oder Funktionen, die einen Situationsterm als Argument haben. Anschaulich bedeutet das: Der Fluent »BallPosition(S0)=(0,0)« verändert seinen Wert durch Ausführen der Aktion »kick« zu »BallPosition(do(kick, S0))=(1,0)«, wenn die Kick-Funktion den Ball einen Meter nach vorn bewegt.
Zusammen mit der Beschreibung der Aktionen, einer Beschreibung, wie sich die Welt durch Ausführen einer Aktion ändert, und einigen weiteren Basisaxiomen lässt sich mit Golog eine Aktionstheorie definieren[6]. Viele Erweiterungen dieses Kalküls[7] ermöglichen es, Golog für den Robocup einzusetzen.
Golog erlaubt es dem Programmierer, den Suchraum dort einzuschränken, wo er ein festes Vorgehen empfehlen kann. Ein Beispiel dafür ist in Abbildung 2 zu sehen. Listing 1 zeigt einen Auschnitt des Angreifer-Programms der Allemaniacs, in dem das entscheidungstheoretische Planen zum Einsatz kommt. Die Planung beginnt mit dem »solve«-Konstrukt, das den Golog-Interpreter anweist einen Plan für den folgenden Programmcode zu erstellen.
Die »nondet«-Anweisung in Zeile 8 gibt verschiedene Aktionsfolgen vor, aus denen der Interpeter die beste (die mit dem höchsten Reward) auswählt. Der Roboter hat die Möglichkeit, sich zwischen einem Dribbling und anschließendem Torschuss »dribble_or_move_kick()« und einem Dribbling zu einer Anzahl von Koordination auf dem Spielfeld zu entscheiden. Aus der Koordinatensammlung wählt »pickBest()« die beste aus. Liegt der Ball direkt vor dem Roboter (Zeile 5), kann sich der Spieler zur Seite drehen und den Ball so bewegen. Alternativ könnte der Roboter ein Dribbling zum Tor wagen (Zeile 12). Abbildung 2 zeigt alle Möglichkeiten, die der Roboter in dieser Situation erwägt.
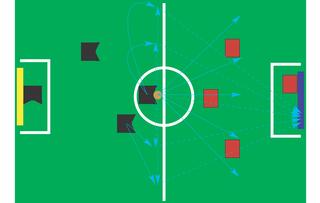
Der Golog-Interpreter ist in Prolog programmiert, genauer in Eclipse-Prolog des Londoner Imperial College[8]. Zum Ausführen von Aktionen aus dem Planungssystem heraus nutzt die Allemaniacs-Software die C++-Schnittstelle von Eclipse. Sie steuern damit die Module der Robotersoftware. Mit dieser Aufgabe beschäftigt sich der Artikel auf Seite 46 ausführlich. (mdö)
| Infos |
|
[1] J. Quinlan, "C4.5 Programs for Machine Learning": Morgan Kafmann, 1993 [2] M. Puterman, "Markov Decision Processes Discrete Dynamic Programming": Wiley, 1994 [3] R. Sutton und G. Barto, "Reinforcement Learning: An Introduction": MIT Press, 1998 und [http://www-anw.cs.umass.edu/~rich/book/the-book.html] [4] H. Levesque, R. Reiter, Y. Lesperance, F. Lin, R. Scherl. GOLOG: "A Logic Programming Language for Dynamic Domains": Journal of Logic Programming, 31 (1-3), 1997 [5] J. McCarthy, "Situations, actions, and causal laws": Technischer Bericht, Universität Standford, 1963 [6] R. Reiter, "Knowledge in Action": MIT Press 2001. [7] Erweiterungen zu Golog: [http://www.cs.toronto.edu/~cogrobo] und [http://www-kbsg.informatik.rwth-aachen.de/research/publications.php] [8] Eclipse-Prolog: A. Cheadle, W. Harvey, A. Sadler, J. Schimpf, K. Shen und M. Wallace, "Eclipse: An Introduction": Technischer Bericht IC-Parc, Imperial College London, 2004, [http://www.icparc.ic.ac.uk/eclipse] [9] F. Dylla, A. Ferrein, G. Lakemeyer, "Acting and Deliberating using Golog in Robotic Soccer - A Hybrid Architecture": Proc. 3rd Cognitive Robotics Workshop, AAAI Press, 2002 |